Assignment: 07-Surface Area
Practice 1: 08-Surface Area Practice
Practice 2: 09- Surface Area Practice 2
Practice 3: 11-Surface Area and Volume Practice
When dealing with surface area, we need to notice that key word area. We are still dealing with just two dimensions. Think of the nets we just used to create our figures. They are a bunch of two dimensional shapes glued together. Defined, surface area is exactly as it sounds, the area on the surface of a three-dimensional shape. To find it, you take the area of each of the sides, and add them together. Think of a rectangular prism.
You can see three different sides. I have labeled them A, B, and C. Remember though, there are also 3 different sides that you can see, which are exactly the same as these. I will unfold this into its net/ I will label all six sides with A, B, and C. notice there will be two As, two Bs, and two Cs. These shapes are the exact same size.
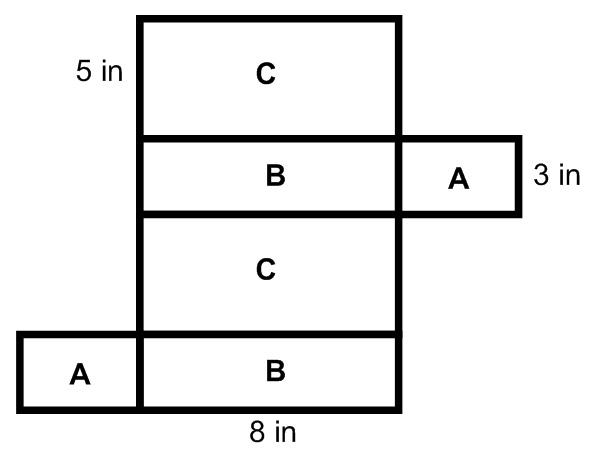Now remember, all opposite sides are equal to each other. Also, as we “fold” it into the rectangular prism, any side that would connect is also equal. If we were to label every side, it would look like this.
This ends up being a lot of repeated numbers in one picture, so most of the time, they will only give you each dimension once, as in the first diagram.
There a couple of different methods we can use to find the surface area of this. We could begin by finding the area of each shape, and them all together.
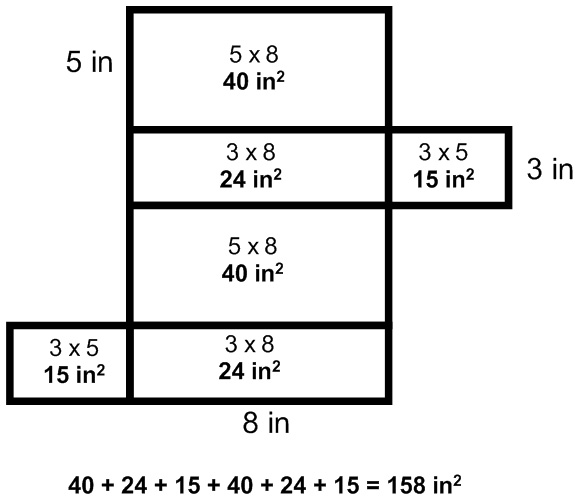Also remember that sides A, B, and C are duplicated, so we could only find the area of those three, and then multiply them together.
A – 3 x 5 = 15
B – 3 x 8 = 24
C – 5 x 8 = 40
15 + 24 + 40 = 79
79 x 2 = 158 in²
This same concept goes for all shapes. Think about the square pyramid.
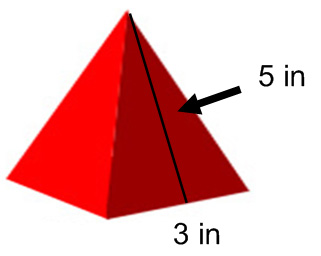Unfold it into the net, and find the area of each shape.
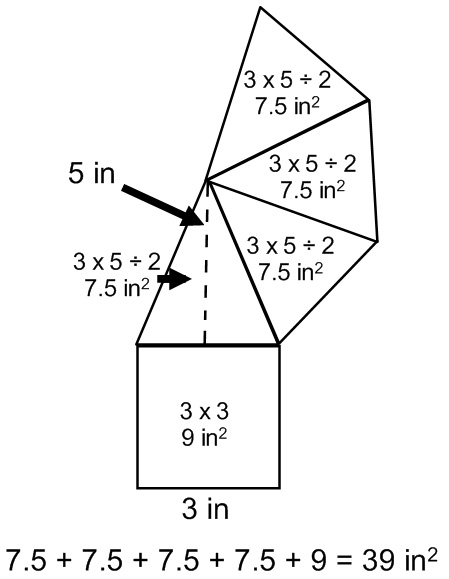Just like the rectangular prism, there is almost always some kind of shortcut with any polyhedron. With this, notice that all four triangles are exactly the same. WE could have found the area of one, multiplied it by four, and added the square.
(3 x 5 ÷ 2) = 3.5
3.5 x 4 = 30
30 + 9 = 39 in²
The final thing to mention would be the units. When dealing with any form of measurement, it is necessary to include the units. Surface area is still dealing with two dimensions, so the units will be squared.
Is there an assignment where you did it like showed steps?
The directions shown above are basically the same thing I showed in class, just drawn out into the shapes. The other way I showed, we just listed the shapes that make the figure. Let’s say a triangular prism.
Triangle
Triangle
Rectangle
Rectangle
Rectangle
From there, you’ll just want to make sure you find the area of each shape, the ones you can see as well as the ones you can’t. Once you have the area of all the shapes, add it together.