Topics:
1.) Multiplying and Dividing Integers
2.) Equations with Integers
3.) Quadrants and Graphing
Multiplying and Dividing Integers
This is something we should only need to spend one day on. Now, I hear what you’re thinking. ”You spent three or four days on adding and subtracting, how is it you’re only going to spend one day on multiplying and dividing?” Simple. It’s that easy. The students have been multiplying and dividing since about third grade. They know that 3×3=9, or more difficult, they could figure out that 12×15=180. With division, they know that 12÷6=2, and again more difficult, they should be able to do the long division for 126÷3=42. Multiplying and dividing with positive and negative numbers adds two simple rules into the mix.
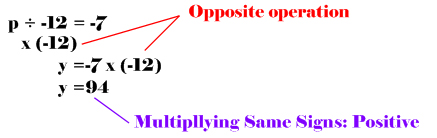
Rule 1: If the signs are the same, whether positive or negative, than the answer is positive.
- 3 x 4 = 12 (positive times positive equals positive)
- 15 ÷ 3 = 5 (positive divided by positive equals positive)
- -2 x -6 = 12 (negative times negative equals positive)
- -32 ÷ -8 = 4 (negative divided by negative equals positive)
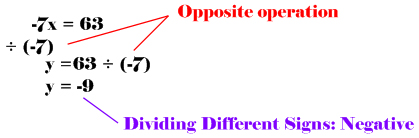
Rule 2: If the signs are different, than the answer is always negative.
- 5 x -6 = 30 (positive times negative equals negative)
- 60 ÷ -12 = -5 (positive divided by negative equals negative)
- -12 x 10 = -120 (negative times positive equals negative)
- -56 ÷ 7 = -8 (negative divided by positive equals negative)
Equations with Integers
Now that we know all of the operations with integers, it’s time we step it up a bit. We’re now going to perform these operations to solve equations. Remember, the two key words when solving equations is Opposite Operations. For a review on solving equations, visit Week 4 of the Math Blog.
Operations with integers is just the same, so long as you remember the rules for the operations and those two key words for solving equations:
Solving an equation with integers involving addition: (Remember, the opposite of addition is subtraction)
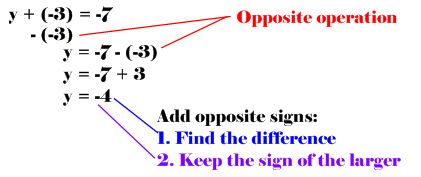Solving an equation with integers involving subtractions: (Remember, the opposite of subtraction is addition)
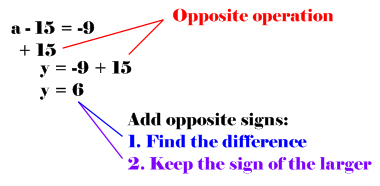Solving an equation with integers involving multiplication: (Remember, the opposite of multiplication is division)
Solving an equation with integers involving division: (Remember, the opposite of division is multiplication)
Quadrants and Graphing
Graphing is another one of those things that the students have been doing for a few now. Each year, a little more complexity gets added to it. This year, we will be dealing with all four quadrants of a coordinate plane.
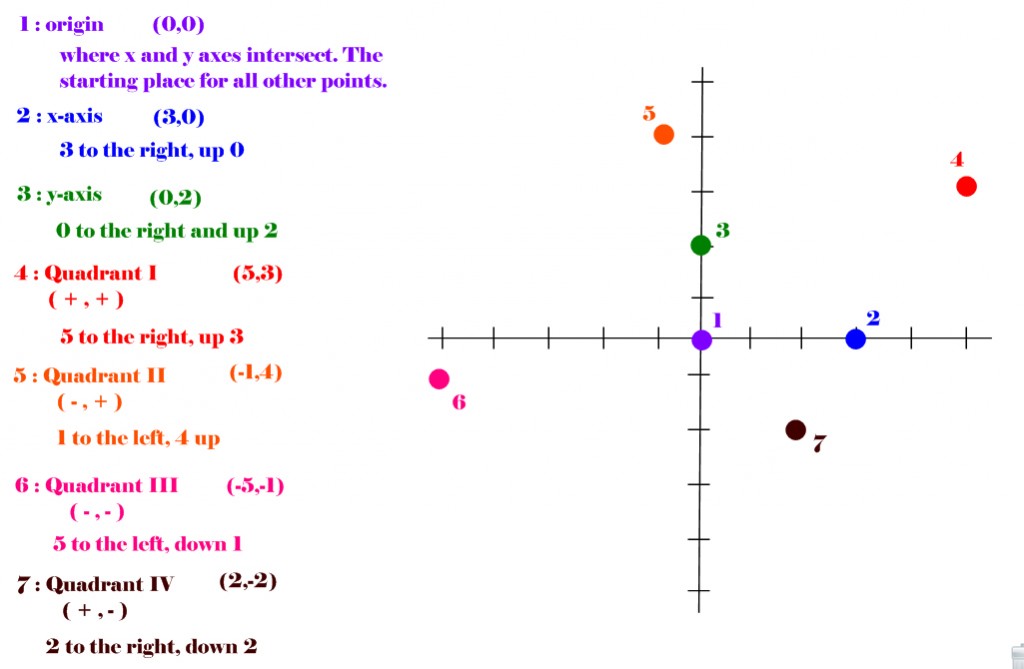
To understand the coordinate plane, we must few understand a few bits of vocabulary. The axes (ax-ees : plural of axis) are the lines which make the divisions between the four quadrants. the x-axis runs horizontally, and the y-axis runs vertically.
You will notice that Quadrant I is the top right. This is the quadrant the students are most familiar with working with. If you are a graphing a coordinate, a set up numbers written for a place on a graph, you always write the ‘x’ number first and the ‘y’ second. A coordinate would look like this (x,y) or as numbers (5,3). Positive ‘x’ numbers tell you to move the right, and positive ‘y’ numbers tell you to move up. If both numbers are positive, the coordinate will always be in the first quadrant.
The quadrants then move counter clockwise. The top left quadrant is Quadrant II. This quadrant is when you have a negative ‘x’ and a positive ‘y’, such as (-1,4).
The bottom let quadrant is Quadrant III. This quadrant is both negative ‘x’ and ‘y’, such as (-5,-1).
The final quadrant in the bottom right is Quadrant IV. A coordinate is in this quadrant when the ‘x’ is positive and the ‘y’ is negative, such as (2,-2).
You have a few other examples we need to discuss. If a coordinate has a zero in either the ‘x’ or ‘y’, it is not in any quadrant, it would just be said that it’s on the axis. (0,2) would be on the y-axis and (3,0) would be on the x-axis. For the coordinate that is zero in both ‘x’ and ‘y’, (0,0), it is called the origin. It’s called the origin because that’s where you should always start when moving to a specific coordinate.
The coordinates I’ve mentioned throughout the lesson here are listed to the right next to where they would be on the coordinate plane. They are also graphed on one with corresponding colors and numbers to the right.
