Assignment 1: Distance between Integers 1
Assignment 2: Distance between Integers 2
In our Understanding Integers lesson we learned how to put all types of integers onto a number line. We also learned about absolute value being a number’s distance from zero, thus the absolute value of -6 would be 6 because it’s 6 numbers away from 0. The next step for us is to be able to figure out two number’s distance from each other.b Typically to do this we would subtract. How far are apart are 9 and 4? Well, 9-4 is 5. It gets a little harder with integers as we haven’t learned subtraction with negative numbers yet.
Let’s take -8 and 3. We want to figure out how far apart these two numbers are. We will start by plotting these two numbers on a number line.
Our first thought could be to just count the number of spaces between our two points. There are 11 spaces between them, therefore the distance between these two points is 11. If they are opposite signs like this, one positive and one negative, you’re basically adding the absolute values together. |-8| is 8, |3| is 3 and 8+3=11.
It’s a little different if the signs are the same. Take -11 and -2. Start again with a number line.
Again, you could just count the number of spaces between the two of them. There are 9 spaces between -11 and -2. Think about our positive numbers though. The distance between 9 and 4 was 5, which is 9-4. I can do the same thing with negative numbers, but remember, because we’re dealing with a distance, we’ll work with their absolute value, because that is their distance to zero. |-11| is 11 and |-2| is 2. We then subtract those. The distance between -11 and -2 is 11-2, which is 9. Knowing this comes in handy when dealing with bigger numbers or numbers that are further apart.
What is the distance between -62 and -21? Well, |-62| is 62, and |-21| is 21,. 62-21=41, therefore the distance between -62 and -21 is 42.
The next step in this lesson is the movement of a number on a number line. If I start with -31 and I want to move a positive 9, I simply want to picture this on a number line. Remember, moving a positive number moves us to the right.
Notice after moving 9 to the right, we end up at -22.
Our final step in all of this all of this, is to be able to put these ideas into real world scenarios. Here’s an example of one for distance:
Johnny was parasailing 23 feet above the water. His brother Mark was SCUBA diving 15 below the water. What is the distance between the two brothers?
To solve these kinds of things, I find it easiest to visualize it by drawing a picture.
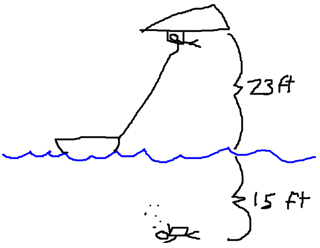This allows us to easily see that finding the distance between the two of them is just a matter of adding the two distances together. Just don’t forget that when talking about a distance below sea level, you’re referring to a negative number, so technically what you are doing here is |23| + |-15| which gives us our 38 feet.
The final type of problem would be real life scenarios for movement. Dealing with only positive numbers of this would be easy considering we should have been doing this for years now. Kaylyn was the flyer for her cheer stunt. The cheer leaders hold her 5 feet in the air. When they release her, they toss her an additional 4 feet. How high did Kaylyn fly? It’s a simple addition problem. She was 5 feet. She flew 4 more. 5+4=9. It’s a little more difficult when dealing with negative numbers. Let’s go back to Mark who was SCUBA diving.
Mark is SCUBA diving 15 feet below sea level. He dives down an additional 12 feet. He then raises by 6 feet. What depth does Mark end at?
Again, I recommend drawing a picture. Basically, what you’re working with is a vertical number line.
The picture allows you see, if he started at 15 feet deep, and swam 12 further, he was 27 feet down which would represented by an integer of -27. If then swam up 6 from there he would move up to 21 feet below sea level, which puts him at -21 feet.