Math Week 29

Topics:
1. Histograms
2. Deviation

Histograms

Similar to a bar graph.  Similar to a line graph. Similar to a line plot. Yet, a different graph all of its own.

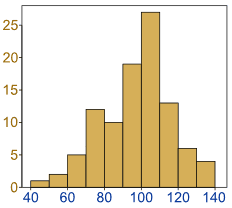A histogram is a graphical display of data using vars of different heights.  Yes, I realize this sounds and looks very similar to a bar graph.  Notice that there are numbers on both the x and y axis.  This is more typical of what you might see on a line graph rather than a bar graph.  Also notice that each bar seems to represent an interval.  This is more typical of what you might see on a line plot.

YAY for smashing three different types of graphs into one!

Let’s display a graph that actually has a bit of meaning to it.  The histogram below represents the height of orange trees in an orchard.  The heights of the trees vary from 100 cm to 340 cm.

Take a careful look at the x axis.  Notice that it counts by 50.  The bar between 100 and 150 represents all the trees that are in between those two heights.  If you look at how high the bar goes, it tells you, of all the trees in the orchard, there are four of them that are between 100 cm and 150 cm.

Some types of questions you might see for reading a histogram:
* Which interval has the most trees in it?
Ans: 200-250
* How many trees are there between 300 and 350?
Ans: 11

Mean Absolute Deviation

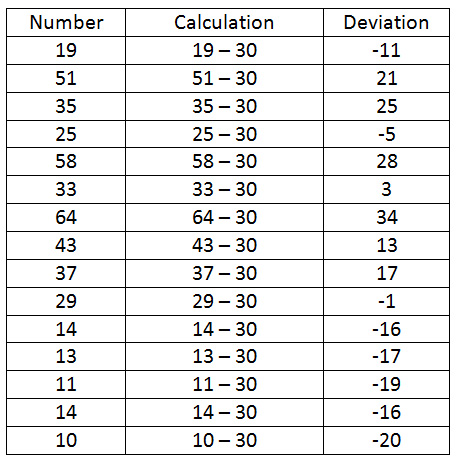
Temporarily taking math out of the picture, the word deviation simply means a change from the normal.  In mathematical terms, deviation is how far a number is away from the norm, in this case, the mean, or average.  The first step in this process is to find the mean of a set of data.  Let’s use the set of data below.

It’s a list of Runs-Batted-In for 15 players on the Seattle Mariners.  To find the average of these numbers, we have to start by adding them all together.

15+51+35+25+58+33+64+43+37+29+14+13+11+14+10 = 456

To find the average we then have to take that total and divide it by the amount of numbers, 15.

456 ÷ 15 = 30.4

Now that we have our average, we are able to calculate the deviation for each of the numbers.  Deviation is dimply the difference between the number and the  average. If a number is higher than the average, than its deviation will be positive.  If a number is below the average, then its deviation will be negative. The one problem we will come across is that we have not learned how to add and subtract with negative decimals.  For this reason, we are going to round our mean to the nearest whole number.

30.2 would round to 30

Below is a chart showing the deviation for each of the numbers in the data set.

The final calculation which will be expected is known as the Mean Absolute Deviation, or MAD for short. This is also known as the Standard Deviation. Simply put, this is the average of all of the deviations we just calculated.  This will require that we add positive and negative integers.  For a review on this topic, click here.

To find the MAD, we have to start by adding all of the deviations together.

-11 + 21 + 25 + -5 + 28 + 3 + 34 + 13 +
17 + -1 + -16 + -17 + -19 + -16 + -20 = 36

The next step in finding the MAD is to divide by the total amount of numbers, 15.

36 ÷ 15 = 2.4

This single number can tell us a lot about the data. The fact that it is positive tells us that there are more numbers above the mean than below.  The closer it is to zero, the more evenly spread out the data is.