Topics:
1. Graphing Shapes
2. Study Guide
3. Practice Questions
4. Test
Graphing Shapes
Previously in the year we have discussed graphing on a coordinate plane. To review this, click the link below:
There are a few different ideas that we introduce in this lesson. The first is if you are given a set of points, can you graph them and be able to identify what shape it makes. Here’s an example. If we were given the four points listed to the right, we would have to graph them on the coordinate plane, as is done, and then be able to identify the shape.
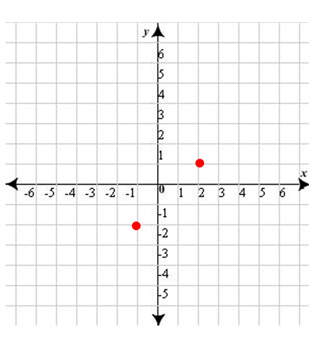
The next idea will be if it tells us the shape it wants. Let’s day they want a square. Given the two points on the graph below, we would have to be able to tell them what the other two vertices would be.
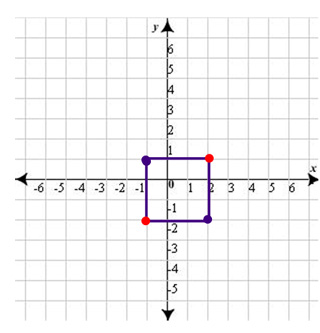
Now, we know that a square has to have four right angles, and all four sides have to be equal. If you were to measure just the horizontal or vertical distances for the two points above, you would see that both those distances would be 3 units. 3 units to the right of (-1, -2) would be (2, -2). 3 units up from that same point would be (-1, 1). That would be the other two vertices: (2, -2) and (-1, 1). We could graph those below and connect the vertices to see that it does in fact make a square.
The other things we will only briefly touch on. They are technically not in our core with the new Common Core, but we have seen them thrown in on the tests at the end of the year, so we do review them. They are the transformation: reflection, rotation, and translation.
Reflection – The axis would act as a mirror. You would need to be able to name the vertices of the new shape, given a reflection. The triangle below is reflected over the y-axis.
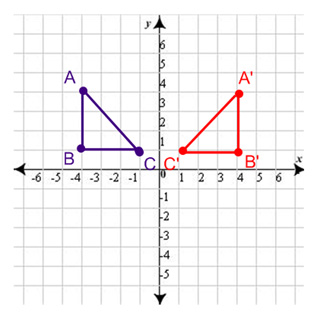Notice the axis acts exactly like a mirror. The point C, which was closest to the axis, is still closest to the axis in the reflection.
Rotation – A rotation is simply the turning of a figure on a certain point. It would be like if you stuck a pin in that point and could spin the rest of the figure around that spot. Look below. The triangle has been rotated 180 degrees on point C.
Notice that point C does not move, and the other points maintained their place. If you were to spin the red triangle back into place, B’ and A’ would be in the same place as B and A respectively.
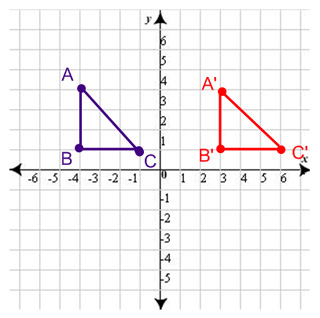
Translation – A translation is a slide, meaning you just move the shape. It doesn’t spin, it doesn’t flip, it just moves. The triangle below has been translated 7 units to the right.
Notice that A’, B’, and C’ are still in their respective places on the triangle. I said the slide was 7 units. If you were to count 7 spaces from B, you would get to B’, and so on with the other points.
TESTING
Our geometry test is this week. We will, as usual, have a study guide we will fill in, and practice questions we will do as a class. I have provided copies of these here, as well as a filled in copy of the study guide.
Unit 7 Study Guide (filled in)