Topics
1. Solving Proportions
2. Understanding Percents
3. Fractions, Decimals, Percents
4. Percent of a Number
Solving Proportions
Now that we know a proportion is simply a pair of equal ratios, solving for them is fairly easy. Look back in the previous week at the ways we said to check if two ratios formed a proportion.
1. If their multiplier is the same.
2. If they can be brought to the same unit rate
3. Cross Multiply
Solving proportions means that our proportion has an unknown value in it. Look below:
![]() We have the first ratio of 8 yards of ribbon for $6. We want to know how many yards of ribbon we can get for $9.00. If our two known values, in this case the bottom numbers, have an easy multiplier, than you could use that method. We could figure out that $6 ∙ 1.5 = $9, so 8 ∙ 1.5 = 12. However, to get that multiplier would be tough. The easier way to solve it is through cross multiplication. It would look like this below:
We have the first ratio of 8 yards of ribbon for $6. We want to know how many yards of ribbon we can get for $9.00. If our two known values, in this case the bottom numbers, have an easy multiplier, than you could use that method. We could figure out that $6 ∙ 1.5 = $9, so 8 ∙ 1.5 = 12. However, to get that multiplier would be tough. The easier way to solve it is through cross multiplication. It would look like this below:
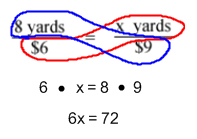 From there, you just need to remember how to solve an equation. Opposite Operations. If you need more of a review than that, click here. Because we are multiplying 6 by x, and the opposite of multiply is divide, we will need to divide the 72 by 6, as shown below:
From there, you just need to remember how to solve an equation. Opposite Operations. If you need more of a review than that, click here. Because we are multiplying 6 by x, and the opposite of multiply is divide, we will need to divide the 72 by 6, as shown below:
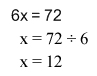 Here is another example, taken from a word problem.
Here is another example, taken from a word problem.
“Before going to France, Maurice exchanged $25 for 20 euros. At that exchange rate, how many euros would he get for $80.”
Understanding Percents
To understand percents, we must first understand the meaning of the word. Per means ‘for each’ and cent means ‘hundred’. To figure out a percent, we must break it into a hundred pieces. Let’s say you take a test with 100 questions. Each question is one part of that hundred, or 1% of the test. If you answer 83 questions correct, you score an 83% because you were correct on 83 of the 100.
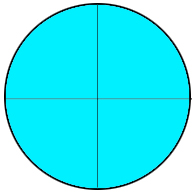
Below is a grid that has 100 squares. 60 of them are green. We can say that 60% of them are shaded. 60/100 is the same as 60%.
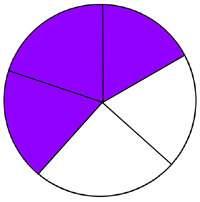
Now, we may have to work shaded areas that are not already broken into 100. Take the circle below for example:
It’s easy to say that 3/5 of that circle is shaded, but we want to know what percent of it is shaded. To do so, we want to make 3/5 an equivalent fraction over 100. To turn 5, the denominator, into 100, you have to multiply it by 20. If I do this to the bottom, I must also do it to the top. It would look like this:
The last thing we need to understand about percents, is how to represent 100% or more. 100% is easy. If the entirety of the item is shaded, no matter how many pieces it’s broken into, you could say that 100% of it is shaded. Example below.
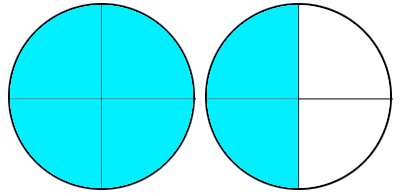
What if I want to represent 150%? 50% is 1/2 of something. My circle is broken into fourths, so 1/2 would be represented by shading two of them. The 100% is still represented by shading a complete circle, so to represent 150% I would need to draw two circles, one of them completely shaded, the other half shaded.
Fractions, Decimals, Percents
We are familiar with fractions. We are familiar with decimals. We are familiar with percents. This lesson is where we realize that fractions, decimals, and percents, are all the same thing: parts of a whole; and it is possible to convert between the three of them.
Converting from a Fraction to a Decimal
Remember, all along we have talked about how a division problem can be represented as a fraction. This is where that comes in handy. To convert a fraction to a decimal, you divide the numerator by the denominator.
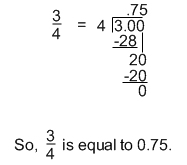 Converting from a Decimal to Percent
Converting from a Decimal to Percent
Converting a decimal to a percent is as easy as times the decimal by 100 or moving the decimal point two places to the right..
0.75 x 100 = 75
So, 0.75 = 75%
Converting from a Fraction to a Percent
Unfortunately, there is no easy way to do this, you have to first convert the fraction to a decimal, and then to a percent.
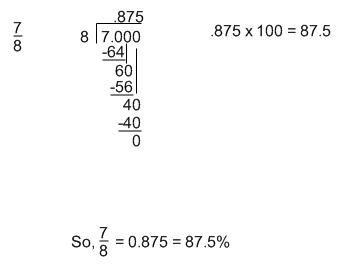 Converting From a Percent to a Decimal
Converting From a Percent to a Decimal
Converting from a percent to a decimal is just the opposite from converting from a decimal to a percent. If you have 80% and you want to make it a decimal, you divide it by 100, or move the decimal point two places to the left.
80 ÷ 100 = 0.80
So, 80% = 0.8
Converting From a Decimal to a Fraction
To be able to convert from a decimal to a fraction, you have to be familiar with your decimal place value. Here is a chart for reminder:
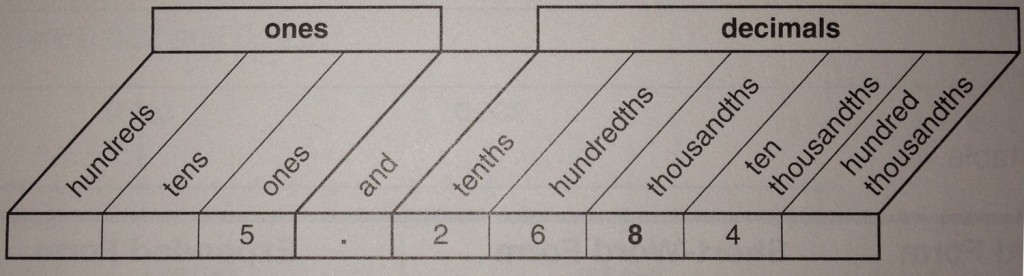 With our previous example 0.8, you would say that eight-tenths. Say that out loud. Now think about that as a fraction. Eight-tenths:
With our previous example 0.8, you would say that eight-tenths. Say that out loud. Now think about that as a fraction. Eight-tenths:
![]() Remember, you may also have to simplify. 8/10 would simplify down to 4/5.
Remember, you may also have to simplify. 8/10 would simplify down to 4/5.
Here’s a few more examples with a bit longer decimals.
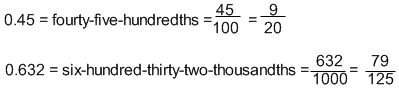 Converting From a Percent to a Fraction
Converting From a Percent to a Fraction
There are a couple of different ways to convert from a percent to a fraction. The first would be to convert from a percent to a decimal, and then the decimal to a fraction. You can simplify that process though, by breaking apart the word percent.
per – for each
cent – hundred
So percent means for each hundred. A fraction bar can also be used to represent the word per, so 45% could be written out 45 / 100. A fraction that just needs simplifying.
Percent of a Number
Finding percent of a number combines two skills that we already know: converting a percent to a decimal, which we learned above, and multiplying decimals, which we learned in Week 6.
If we want to take the problem, as below:
37% of 51
The first step is to convert the percent to a decimal. the second step is to think of the of as multiply, so:


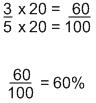

I have found several errors in the last lesson of Math Week 13. First of all, 37%, divided by 100, would be 0.37, not 0.35. Another error is that when you multiplied, instead of putting your incorrect answer of 0.35, you put 0.31 as the multiplier. After doing it correctly, I’ve concluded that the correct answer of 37% of 51 would be 18.87, not 8.61.
You have no idea how long these Math entries can take to write, so first off, I’m super happy to see that I have students reading them!
Secondly, I will admit that, because they do take so long, by the time I get to the end, I don’t proofread as much as I do in the beginning, so I am grateful that you’ve been my editor-in-chief! Thanks, Austin!
I LOVE, LOVE, LOVE this math blog. It makes it so easy to help with homework. Thank you for taking the time to put it together.