Assignments: 05-Dividing by a Whole Number
This is the lesson where we do away with remainders. No more will we say that a 30÷7=4r2. Nope. Now we follow a a bit more complex algorithm. Let’s take a look at 196÷32. With the old algorithm it would have looked like this:
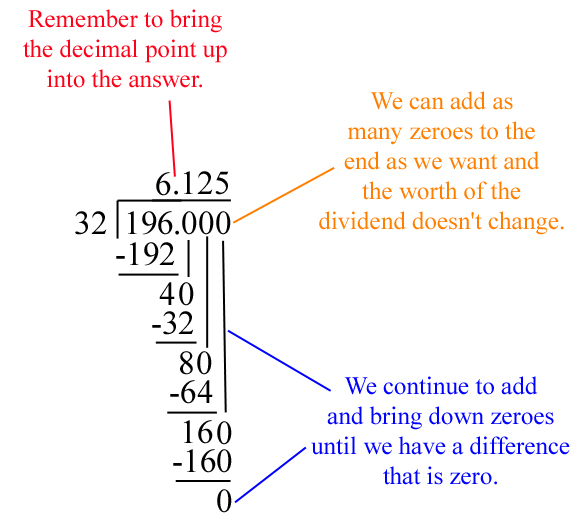
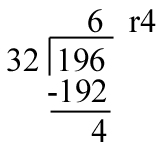 One thing that we already know is that the decimal point in a whole number comes right at the end of it. So, 196 = 196.0. With this knowledge, we can now extend out our problem until we find a more complete solution. One key thing to remember, is wherever we put the decimal in the dividend (the number on the inside) we have to jump the decimal up into the answer at that same spot. It would look more like this:
One thing that we already know is that the decimal point in a whole number comes right at the end of it. So, 196 = 196.0. With this knowledge, we can now extend out our problem until we find a more complete solution. One key thing to remember, is wherever we put the decimal in the dividend (the number on the inside) we have to jump the decimal up into the answer at that same spot. It would look more like this:
 There will be sometimes that we come across answers that seems to keep going on and on. If it is a repeating decimal, such as if you were to do 1÷3 which equals 0.333333333…., you can put a line over the first 3 and that tells us that number keeps repeating forever. It would look like this:
There will be sometimes that we come across answers that seems to keep going on and on. If it is a repeating decimal, such as if you were to do 1÷3 which equals 0.333333333…., you can put a line over the first 3 and that tells us that number keeps repeating forever. It would look like this:
If it is not a repeating decimal, but still seems to not stop, then we can round it. Often times, the hundredth is the furthest we will ever need on a decimal. Remember though, to be able to round to the hundredth, we need to go one additional place so we know whether to round up or leave it the same. Anything less than 5 stays the same, anything 5 or greater rounds up. Let’s look at the original problem I mentioned, 30÷7. It would equal 4.28571….. To round to the hundredth, which is the currently the 8, we need to look at the digit one past it, which is a 5. A 5 tells us to round up, so our answer would be 4.29.
