Topics:
1. Solid Figures
2. Surface Area
3. Volume
Solid Figures
I did mostly cover this topic last week. There were a few things I added to it, so please take a look at it before you continue
We will also be building some of the figures. Specifically, we will build a cube, a rectangular prism, a triangular prism, and a square pyramid. I will have a few others they can build in their free time if they want, but those are four we are going to focus on. Here is a copy of those four Nets.
Surface Area
When dealing with surface area, we need to notice that key word area. We are still dealing with just two dimensions. Think of the nets we just used to create our figures. They are a bunch of two dimensional shapes glued together. Defined, surface area is exactly as it sounds, the area on the surface of a three-dimensional shape. To find it, you take the area of each of the sides, and add them together. Think of a rectangular prism.
You can see three different sides. I have labeled them A, B, and C. Remember though, there are also 3 different sides that you can see, which are exactly the same as these. I will unfold this into its net/ I will label all six sides with A, B, and C. notice there will be two As, two Bs, and two Cs. These shapes are the exact same size.
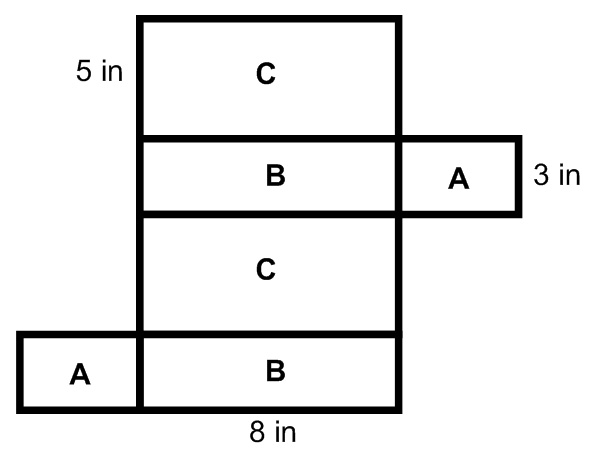Now remember, all opposite sides are equal to each other. Also, as we “fold” it into the rectangular prism, any side that would connect is also equal. If we were to label every side, it would look like this.
This ends up being a lot of repeated numbers in one picture, so most of the time, they will only give you each dimension once, as in the first diagram.
There a couple of different methods we can use to find the surface area of this. We could begin by finding the area of each shape, and them all together.
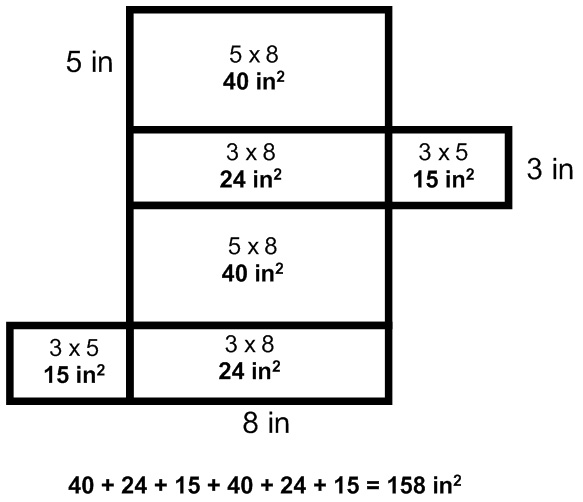Also remember that sides A, B, and C are duplicated, so we could only find the area of those three, and then multiply them together.
A – 3 x 5 = 15
B – 3 x 8 = 24
C – 5 x 8 = 40
15 + 24 + 40 = 79
79 x 2 = 158 in²
This same concept goes for all shapes. Think about the square pyramid.
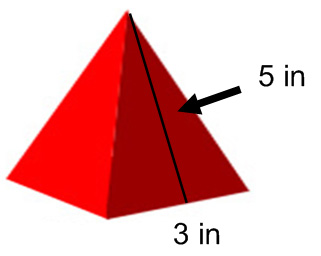Unfold it into the net, and find the area of each shape.
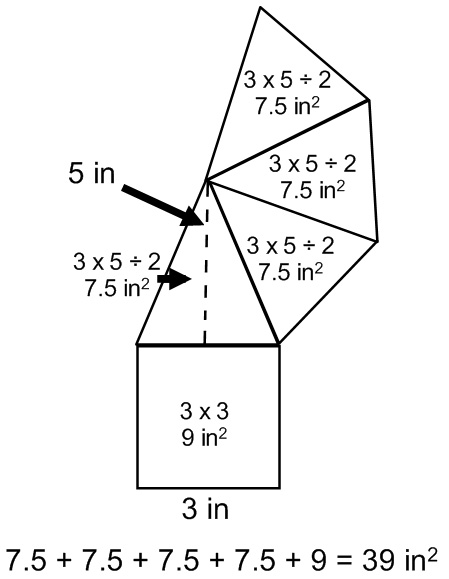Just like the rectangular prism, there is almost always some kind of shortcut with any polyhedron. With this, notice that all four triangles are exactly the same. WE could have found the area of one, multiplied it by four, and added the square.
(3 x 5 ÷ 2) = 3.5
3.5 x 4 = 30
30 + 9 = 39 in²
The final thing to mention would be the units. When dealing with any form of measurement, it is necessary to include the units. Surface area is still dealing with two dimensions, so the units will be squared.
Volume
Once you are familiar with area, volume comes a bit easier. There is just one simple formule.
V = B x h
Notice, I used a capital B. This represents the area of the base of a three-dimensional figure. It is the large B to differentiate it from the base of a two-dimensional figure, which we would write as b. The differentiation is necessary when dealing with things the volume of a triangular prism. Remember, the formula for area of a triangle is a = bh/2. You don’t want to confuse your B, for area of the base of the prism, with the little b, for the length of the base of the triangle. Let’s begin by looking at a cube.
The base of a cube is a square. To find the area of that square, you do length times width, which would be 4 x 4 = 16 in². To finish the formula for volume, we multiply that by the height, which being a cube is also 4: 16 x 4 = 64 in³. Notice the units are now cubed. This is because we are dealing with all three dimensions: width, height, and depth.
Next, let’s look our rectangular prism again, except this time, let’s find the volume of it.
The base of a rectangular prism is a rectangle. Really, you could choose any of the rectangles to start with. For consistency, let’s start with B. Remember, the area of B was 8 x 3 = 24 in². We would then multiply that by the remaining dimension of 5: 24 x 5 = 120 in³.
The final shape we will have to worry about finding the volume of this year is the triangular prism.
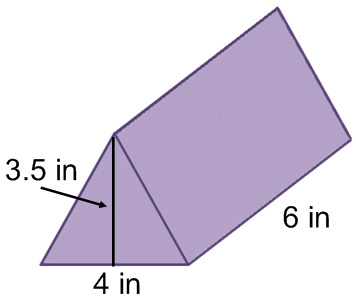The base of a triangular prism is the triangle. To find the area of that triangle, we would do 3.5 x 4 / 2 = 7 in². We then multiply that by the height: 7 x 6= 42 in³.