Topics:
1. Two-Dimensional Shapes
2. Perimeter
Two-Dimensional Shapes
square – four equal sides, four 90 degree angles; a special type of rectangle
rectangle – two sets of equal sides, four 90 degree angles; a special type of parallelogram
parallelogram – two sets of equal, parallel sides
rhombus – two sets of parallel sides, all four sides equal
equilateral triangle – all three sides equal
right isosceles triangle – two sides equal; one 90 degree angle
scalene triangle – no sides are equal
pentagon – five sides figure
hexagon – six sided figure
octagon – eight sided figure
regular – simply put, it means all sides are equal. A square would be a regular rectangle. An equilateral triangle would be a triangle. A regular pentagon would just mean that all five sides of the pentagon are the same length.
Perimeter
I like to introduce the idea of perimeter by giving it a real world application. The troops above have been ordered to “Clear the perimeter” before moving in. What does this order tell them to do? To understand their command, we have to know what the word perimeter means.
Perimeter is the length of the distance around a closed geometric figure. Now closed simply means that all of the edges of the shape are connected to another edge. Each of the shapes listed in the two-dimensional figures are closed shapes. To be able to measure the perimeter around them, we either need a tool to measure, or a shape that gives us the measurement. For our purposes, the required distances will be given to us. It may not give us every measurement, but it will give us enough to figure out the others.
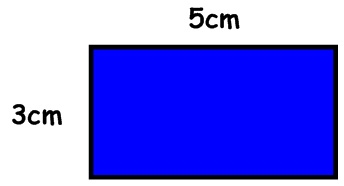
If we were asked to find the perimeter of the above rectangle, would we have all the required information? Yes. Because the question told us it is a rectangle, we know that the opposite sides are equal length. If we add the two distances it gives us we get 5 + 3 = 8. Because there are two of each, we could simply add it again, 5 + 3 + 5 + 3 = 16, or we can add it once and multiply it, 2(5 + 3) = 16cm. Remember, in the final answer, it is always important to include the units of measure.
We might not always be given a picture of the shape. The directions might tell us to find the perimeter of a regular hexagon with sides length 3 in. There are two necessary words in that question, hexagon, which tells us that the shape will have six sides, and regular, which tells us that all six sides are equal. To solve it then, we times the length of the sides by the number of sides. 3 x 6 = 18 in.
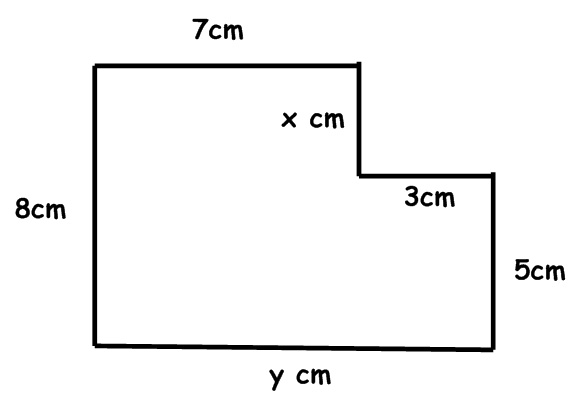
The other challenge we will have thrown at us is finding distances that are not given.
If you study the above diagram, you will notice that there are two distances, x and y, that are not given. It is our job to figure them out. Let’s look at y first. It is the entire length of the horizontal edge. If you look above it, we have two horizontal lengths that would equal it, 7 cm and 3 cm. To find y, we just have to add those together 7 + 3 = 10 cm.
The other distance is x. The entire vertical length is equal to 8 cm. You are told part of it, 5 cm, and your job is to figure out what the other part would be. You can think about it as an equation 5 + x = 8, and you have to solve for x. To do this, we follow the rule for solving equations and use the opposite operation, you end up with x = 8 – 5, so x = 3 cm.