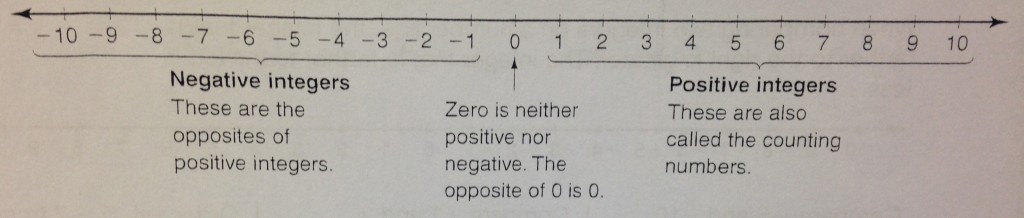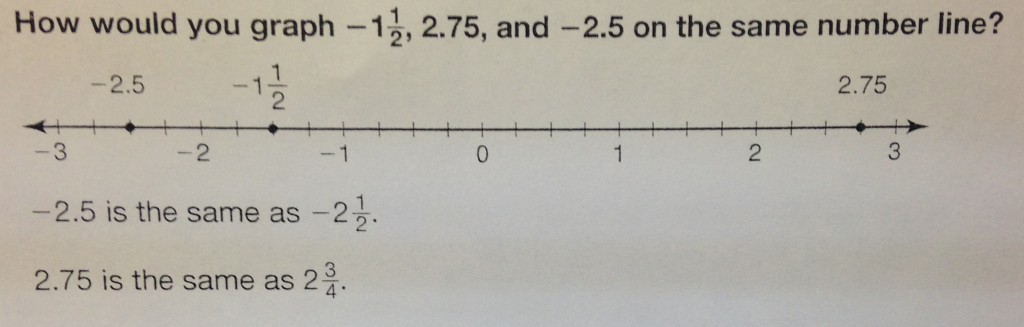Topics
1. Unit 5 Pretest
2. Understanding Integers
3. Compare and Order Integers
4. Rational Numbers
5. Quiz
Understanding Integers
Integers - any whole number, positive, negative or 0.
Positive Integer – Any whole number greater than 0. Opposite of negative.
Negative Integer – Any whole number less than 0. Opposite of positive.
Zero – Neither positive nor negative. The opposite of 0 is 0.
If we were look at a number line, the positive numbers will always go to the right, the negative numbers will always go to the left. Zero will be right in the middle of the two.
Absolute Value - a numbers distance away from zero. Absolute value is always positive as a distance is always a positive thing. Absolute value is represented by two vertical lines around a number: |-6|
Looking at the number line above, point M is located at -6. Because it is 6 units away from 0, it’s absolute value is 0, or |-6| = 6.
Point P is located at 3 on the number line. Because it is 3 units away from 0, it’s absolute value is 3, or |3| = 3.
Questions for this unit might look like this:
Look at the number line above. Write the integer that each point is located on. Also give its opposite and absolute value.
A : The integer is 0. The opposite is 0. The absolute value is 0.
B : The integer is -2. The opposite is 2. The absolute value is 2.
D : The integer is 6. The opposite is -6. The absolute value is 6.
Compare and Order Integers
A quick review of the necessary symbols:
> Greater than
< Less than
= Equal
When comparing integers on a number line, the number that is farther to the right is greater. The integer that is farther to the left is less.
If we were to compare 2 and -1, the 2 is farther to the right, so 2 is larger. Also, no matter what numbers are being used, a positive number is always greater than a negative number.
If we were to compare -6 and -10, -6 is farther to the right, so -6 is larger. When comparing two negative numbers, the integer with the smaller absolute value is less (ignoring the sign, the smaller number actually has the larger value).
There is a couple of ways to think about ordering integers. First off, you could look at them on a number line. Remember the numbers further to the left are lesser, and the numbers further to the right are greater, so if we were to want to order -4, 0, and -7, your thought process might be this:
- -7 is furthest to the left, so it’s first.
- 0 is furthest to the right, so it’s last.
- -4 is in between them, so it’s in the middle.
- -7, -4, 0
Rather than drawing a number line every time, you could also just use the comparison rules. Negative are always bigger than positive, smaller negative numbers are greater than larger ones. So if I wanted to compare 0, -10, 2 and -4, my thought process might look like this:
- 2 is the only positive number, so it’s going to be largest.
- 0 will be larger than any negative numbers.a
- If you look at -4, and -10, -4 has the smaller number, so it will be larger, making -10 the smallest.
- -10, -4, 0, 2
Rational Numbers
We have previously compares and ordered fractions. We have previously compared and ordered fractions. This unit, we compared and ordered integers. Rational numbers basically takes all of the concepts and throws them into one lesson.
A rational number is any number that can be made by dividing two integers. Another way to think of it, is any number you could place on a number line. This includes whole numbers, integers both positive and negative, positive and negative fractions, and positive and negative decimals. It is possible to graph all of these on the same number line.
Example:
Remember, with fractions, -2.5 is in between -3 and -2, so make sure it gets put in the correct place. A common mistake make would be putting it to the right of -2, because that’s what you would do with postivie numbers. Be sure to not make this mistake. It goes to the left of -2 and to the right of -3.
Honestly, the easiest way to graph, compare or order any rational numbers is to make sure they are all in the same form. Don’t try to compare fractions to decimals, convert them so they are either both fractions or both decimals. Beyond that, they follow the same rules.
- On a number line, the numbers further to the left are lesser, and the numbers further to the right are greater.
- When comparing positive and negative numbers, positive numbers are always greater.
- When comparing positive numbers, the larger number is greater.
- When comparing negative numbers, the smaller number is greater, even with fractions and decimals.