Now that we know a proportion is simply a pair of equal ratios, solving for them is fairly easy. Look back in the previous week at the ways we said to check if two ratios formed a proportion.
1. If their multiplier is the same.
2. If they can be brought to the same unit rate
3. Cross Multiply
Solving proportions means that our proportion has an unknown value in it. Look below:
We have the first ratio of 8 yards of ribbon for $6. We want to know how many yards of ribbon we can get for $9.00. If our two known values, in this case the bottom numbers, have an easy multiplier, than you could use that method. We could figure out that $6 ∙ 1.5 = $9, so 8 ∙ 1.5 = 12. However, to get that multiplier would be tough. The easier way to solve it is through cross multiplication. It would look like this below:
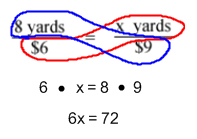From there, you just need to remember how to solve an equation. Opposite Operations. If you need more of a review than that, click here. Because we are multiplying 6 by x, and the opposite of multiply is divide, we will need to divide the 72 by 6, as shown below:
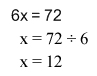Here is another example, taken from a word problem.
“Before going to France, Maurice exchanged $25 for 20 euros. At that exchange rate, how many euros would he get for $80.”
