Assignment: Area of Irregular Shapes
We have learned how to find the area of rectangles and triangles. To review those click the links below:
This lesson combines both of those ideas into finding the area of irregular shapes. Take a look at the shape below:
To find the area of a shape like that, you simply need to decompose it into shapes we know how to find the area of. This particular shape would be divided into two rectangles; more specifically, a square and a rectangle.
From there we are able to easily find the area of the two shapes.
Square: 3 x 3 = 9
Rectangle: 9 x 2 = 18
At that point, you simply add them together and you have the area of your irregular shape.
9 + 18 = 27 in²
It doesn’t matter how complex the irregular shape gets, the concept is the exact same.
Start be separating the complex shape into simple shapes that we know.
When we decompose a shape like this, we may end up having to transpose some of the distances so we have all the information we need. notice the bottom rectangle only has about half it’s length measure at 6. This is because we have 4 for the left tower, and 5 for the right tower. This tells us that the bottom rectangle is actually 15 long. In this irregular shape, then, we have four shapes
Triangle – 4 x 4 ÷ 2 = 16 ÷ 2 = 8
Rectangle – 12 x 4 = 48
Rectangle – 6 x 15 = 90
Rectangle – 5 x 4 = 20
We then add them together and we have the area of our irregular shape.
8 + 48 + 90 + 20 = 166 un²
The other idea I want to bring up is the idea of using shapes that we know to find the area of shapes we don’t know. For example, this pentagon:
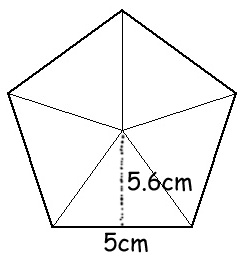We know how to find the area of the triangle: 5 x 5.6 ÷ 2 = 14. There are five triangles that make up this pentagon, so we can then take the area of one triangle, and times it by 5 to get the area of the pentagon.
14 x 5 = 70 cm²