Assignment: 02-Area of Squares and Rectangles
Practice: 04-Perimeter and Area Practice
Area is defined as the amount of space inside the boundaries of a two-dimensional shape. Look at the square below.
You will notice in the larger square above there are 9 smaller squares. This is the space we are dealing with. When we talk area, we talk in square units, or un². So we could say the area of this square is 9 un². Those 9 little squares are where we get that area.
Let’s look at it a bit differently. There are two measurements we need to be familiar with on a rectangle: the length and the width. The length is the distance across the base of the figure, and the width could also be thought of as the height.
Another way to calculate is area is to take the length and multiply it by the width. If we look at our original square, these two measurements are both 3 units. If you were to calculate 3×3, you would get the same area of 9 un².
This same formula works for all rectangles. Take a look at the rectangle below.
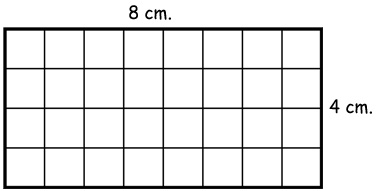We could just count all the squares in the rectangle and get 32, but the more and more we get, the harder and harder it would be to just count them. This is where the formula really comes into play. If we do 8×4, we would get the same 32 as if we had counted it. Notice that this one has actually been given a unit, centimeters, therefore, our answer would be 32 cm².
Now the one level of difficult we have to add to this, is when our measurements have either fractions or decimals. Before we get any further into it, if you need to review multiplying with fractions and decimals, click below.
This is when the formula is really necessary. Let’s say we’re not given a picture, we’re just given the question:
What is the area of a rectangle with length of 3.2 in. and width of 4.5 in?
All we have to do is plug those numbers into our formula: length x width, and we have our answer; 3.2 x 4.5
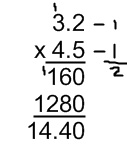So the area of a rectangle whose length is 3.2 in. and whose width is 4.5 in, would be 14.4 in².
The final thing we might be asked to do is to find one of the dimensions of a rectangle if we are given the area. Let’s say we have a rectangle whose area is 48 m². If this rectangle has a length of 8 m, what is its width? We have to think about this as an equation. We know that length x width = area. Fill in the numbers we know. 8 x width = 48 m². To solve this, we solve the equation: opposite operation. The opposite of multiplying by 8 is dividing by 8, so 48÷8 = 6. the width of the rectangle is 6 m.