A ratio is a comparison between the amount of two different things. It is probably the concept we cover in sixth grade that is used the most throughout our lives. Miles per hour, dollars per pound, etc.
Study the picture below.
Looking at the picture, we can all agree that there are 5 apples and 4 zucchini. If we were asked the question,”What is the ratio of apples to zucchini?” The response comes entirely from those numbers. It would be 5 to 4. Notice that the first object asked was apples, so the first number I put is the number of apples. Another of the basics for ratios is knowing that there are three different ways that we can write them. I have already shown you the first, we can use words, “5 to 4″. We can also write it, replacing the word to with a colon. It would look like this “5:4″. Finally, we can write it as a fraction “5/4″.
Here is another example. Count the number of x’s and o’s. The ratio of x’s to o’s is 5 to written in its three forms is shown below.
The other part of this lesson is equivalent ratios. Equivalent ratios works in the exact same way that equivalent fractions did. We could multiply or divide it, so long as we do the same thing to both numbers. Let’s take this ratio of tigers to lions.
This ratio tells me that for every 10 tigers there are 4 lions. This means if I have 20 tigers, meaning I multiplied the number of tigers by 2, I would have 8 lions, also multiplied by 2. So an equivalent ratio 10 10:4 could be 20:8. I could also multiply them by 3, 30:12, or 4, 40:16. This could continue going on for however long we wanted, and so long as multiply both numbers by the same thing, it will be an equivalent ratio.
As I previously said, we can also divide them. Just like fractions have a simplest form, ratios do as well. If we take the ratio of 10 tigers to 4 lions, we can use our cake method to reduce it to its simplest form, just as we did with fractions.
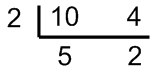So, if there are 10 tigers to every 4 lions, then we can reduce that to there being 5 tigers for every 2 lions.