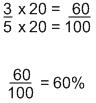To understand percents, we must first understand the meaning of the word. Per means ‘for each’ and cent means ‘hundred’. To figure out a percent, we must break it into a hundred pieces. Let’s say you take a test with 100 questions. Each question is one part of that hundred, or 1% of the test. If you answer 83 questions correct, you score an 83% because you were correct on 83 of the 100.
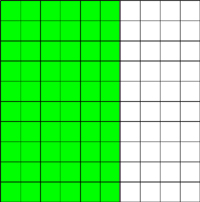
Below is a grid that has 100 squares. 60 of them are green. We can say that 60% of them are shaded. 60/100 is the same as 60%.
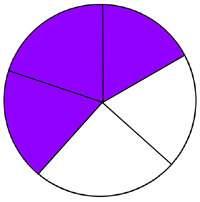
Now, we may have to work shaded areas that are not already broken into 100. Take the circle below for example:
It’s easy to say that 3/5 of that circle is shaded, but we want to know what percent of it is shaded. To do so, we want to make 3/5 an equivalent fraction over 100. To turn 5, the denominator, into 100, you have to multiply it by 20. If I do this to the bottom, I must also do it to the top. It would look like this:
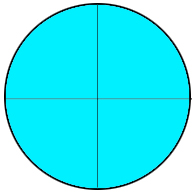
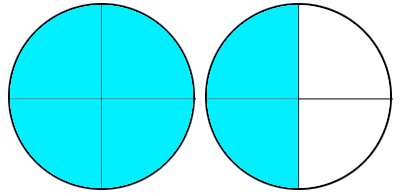
The last thing we need to understand about percents, is how to represent 100% or more. 100% is easy. If the entirety of the item is shaded, no matter how many pieces it’s broken into, you could say that 100% of it is shaded. Example below.
What if I want to represent 150%? 50% is 1/2 of something. My circle is broken into fourths, so 1/2 would be represented by shading two of them. The 100% is still represented by shading a complete circle, so to represent 150% I would need to draw two circles, one of them completely shaded, the other half shaded.