Remember that a factor is either a number you multiply to get a product, or a number that evenly divides into another. Both mean basically the same thing, just worded a little different. For this lesson, we also need to remember that a prime number is a number that has only two factors 1 and itself. Though the list is endless, a few of the prime numbers are 2, 3, 5, 7, 11, 13, 17, and 19. A composite number is any number that has more than 2 factors: 4, 6, 8, 9, 10, 12, etc.
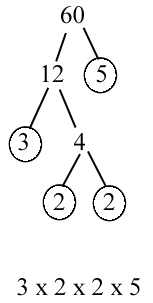
Prime factorization, then, is the prime numbers you would multiply together to get a certain product. For example, 15 is a composite number, but we could multiply the prime numbers 3 and 5 together to get it, so 15′s prime factorization is 3×5. A more complex example might be 60. 60=12×5, but 12 is not prime, so you need to break it down, 60=12×5=4x3x5. The numbers are still not all prime, so we need to break it down one further 60=4x3x5=2x2x3x5, so our prime factorization for 60 is 2x2x3x5. The easiest way to represent this process is through what we call a factor tree. The factor tree for 60 would look like this:
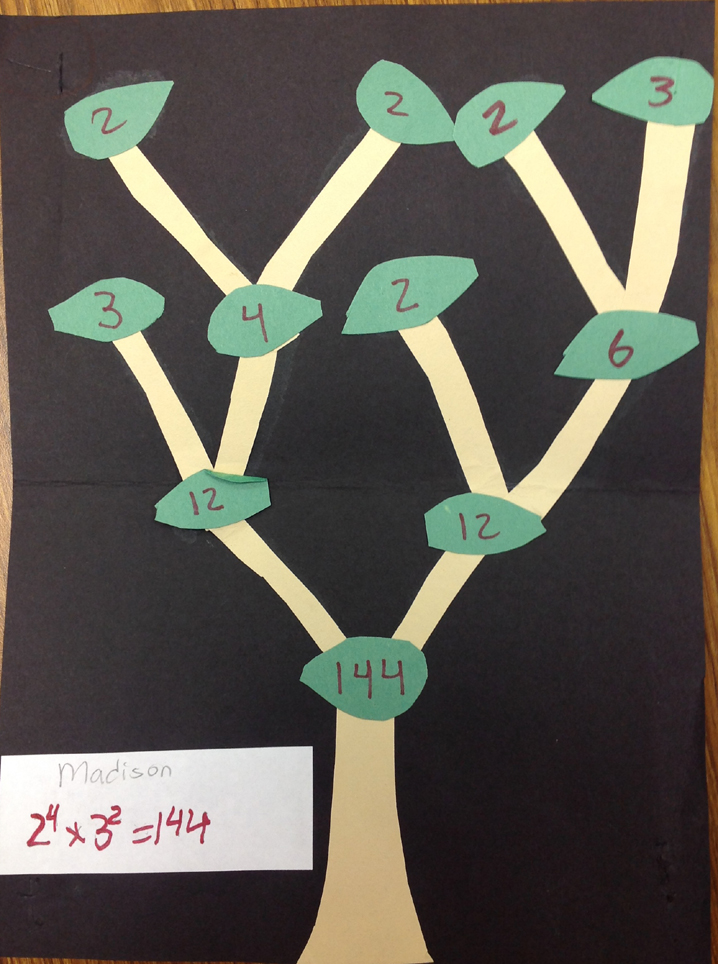
The students will practice this by selecting any number between 100 and 200 that has at least four prime factors, and creating a factor tree similar to what is pictured below: