Topics:
1. Area of Squares and Rectangles
2. Area of Triangles and Parallelograms
3. Solid Figures
Area of Squares and Rectangles
Area is defined as the amount of space inside the boundaries of a two-dimensional shape. Look at the square below.
You will notice in the larger square above there are 9 smaller squares. This is the space we are dealing with. When we talk area, we talk in square units, or un². So we could say the area of this square is 9 un². Those 9 little squares are where we get that area.
Let’s look at it a bit differently. There are two measurements we need to be familiar with on a rectangle: the length and the width. The length is the distance across the base of the figure, and the width could also be thought of as the height.
Another way to calculate is area is to take the length and multiply it by the width. If we look at our original square, these two measurements are both 3 units. If you were to calculate 3×3, you would get the same area of 9 un².
This same formula works for all rectangles. Take a look at the rectangle below.
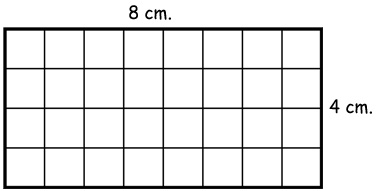We could just count all the squares in the rectangle and get 32, but the more and more we get, the harder and harder it would be to just count them. This is where the formula really comes into play. If we do 8×4, we would get the same 32 as if we had counted it. Notice that this one has actually been given a unit, centimeters, therefore, our answer would be 32 cm².
Now the one level of difficult we have to add to this, is when our measurements have either fractions or decimals. Before we get any further into it, if you need to review multiplying with fractions and decimals, click below.
Multiplying Fractions – Math Week 10
Multiplying Decimals – Math Week 6
This is when the formula is really necessary. Let’s say we’re not given a picture, we’re just given the question:
What is the area of a rectangle with length of 3.2 in. and width of 4.5 in?
All we have to do is plug those numbers into our formula: length x width, and we have our answer; 3.2 x 4.5
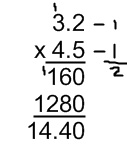So the area of a rectangle whose length is 3.2 in. and whose width is 4.5 in, would be 14.4 in².
The final thing we might be asked to do is to find one of the dimensions of a rectangle if we are given the area. Let’s say we have a rectangle whose area is 48 m². If this rectangle has a length of 8 m, what is its width? We have to think about this as an equation. We know that length x width = area. Fill in the numbers we know. 8 x width = 48 m². To solve this, we solve the equation: opposite operation. The opposite of multiplying by 8 is dividing by 8, so 48÷8 = 6. the width of the rectangle is 6 m.
Area of Triangles and Parallelograms
I want you to take a look at the rectangle below:
Using the formula we previously learned in Area of Squares and Rectangles, l x w, we could calculate that the area of this rectangle is 15 in². Now what happens if we draw a diagonal line from one corner to the other and then break it apart. Like so:
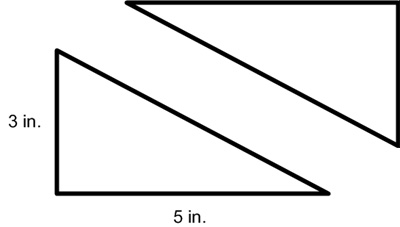
You’ll notice we now have two triangles. This brings us to our formula for finding the area of a triangle. We simply use the same formula we did for rectangles and then we split it in half.
Rather than referring to these as length and width, we refer to them as base and height. This comes in handy if the triangles are skewed as below. Notice, the base is still the bottom, but the height comes up the middle of the triangle rather than one of the sides.
We now follow the formula,
Solid Figures
Cube – 6 sided figure, all sides are squares, all 90 degree angles
Rectangular Prism – 6 sided figure, all sides are rectangles, all 90 degree angles
Rectangular Pyramid – Rectangle base with four triangle steadily leaning toward one vertex at the top
Cylinder – Top and bottom are circles, with a rectangle wrapped around the edges
Cone – Bottom is a circle, edge steadily moves to a single point at the top
Sphere – a three-dimensional circle; a ball
There are just a few vocabulary words I would like to make sure we are familiar with.
Vertices (s. Vertex) – the corners of a three dimensional shape. When we name vertices, we usually just use the letter that is labeling it to name it.
Edges – the line between two vertices. Edges are usually identified by listing the two vertices that are connected.
Faces – the two-dimensional figures creating the sides of a three-dimensional figure. Faces are usually named by listing the vertices that make that face.
Take a look at the figure below:
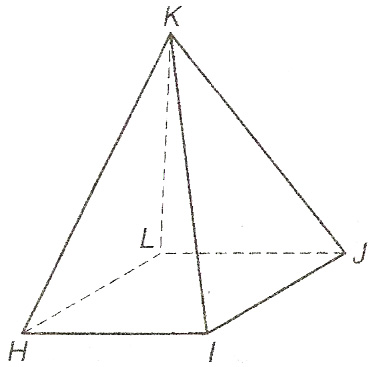This polyhedron (many sides figure) above is a square pyramid, a form of a rectangular pyramid. Remember, a square is just a special type of rectangle. If we were to name all of the parts of this, it might look like this:
Vertices – H, I, J, K, L
Edges – HI, IJ, LJ, HL, HK, IK, LK, JK
Faces – HIK, IJK, JKL, HKL, (The four trangles), and HIJL (the square)