Topics:
1. Adding Integers
2. Subtracting Integers
Adding Integers
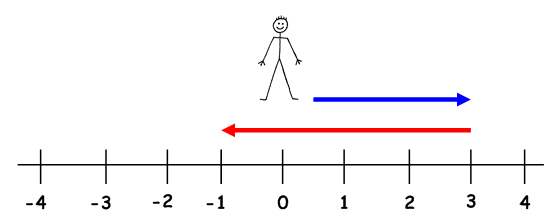
Now that we understand positive and negative numbers, it’s time to start learning the operations with them. If we wanted to add integers on a number line, we could use the idea of the walking man. If we’re adding a positive number, the walking man moves to the right, if we’re adding a negative the walking man moves to the left. Let’s look at 3 + -4. Below is a picture of the walking man. The walking man always begins his journey on zero. He then moves 3 to the right for the positive 3, then 4 to the left for the negative 4. The result is -1.
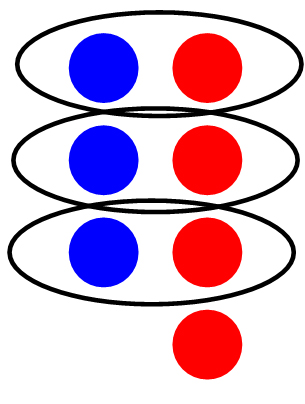
You also need to remember that positives and negatives are opposite, and when opposite numbers meet, they cancel each other out. Following the same idea as the picture above, remember that blue represented positive, and red represented negative. If put 3 positives and four negatives side by side with each other, we end up with just one negative with a partner to cancel it out, leaving us with the answer of -1.
Eventually we will have to get past the point of drawing pictures though. When you get into something like -14 + 32, that would be a lot of dots to draw. This is when we introduce the rules for adding integers.
If the signs are the same: add the numbers and keep the sign.
- 8 + 9 : 8 + 9 = 17, and because they are both positive it stays positive, 17.
- -6 + -12 : 6 + 12 = 18, and because they are both negative, the answer is -18.
If the signs are different: find the different between the numbers and keep the bigger sign.
- -8 + 6 : 8-6 = 2 : The negative is the larger number, so it’s -2.
- 14 + -5 : 14-5 = 9 : The positive is the larger number so it’s 9.
Subtracting Integers
When subtracting integers, we really want to think of the subtraction sign meaning the word opposite. 7 is a positive number, so -7 is just the opposite of that, a negative number. If I were to have -(-8), then I want the opposite of a negative number which is positive, so -(-8) = 8
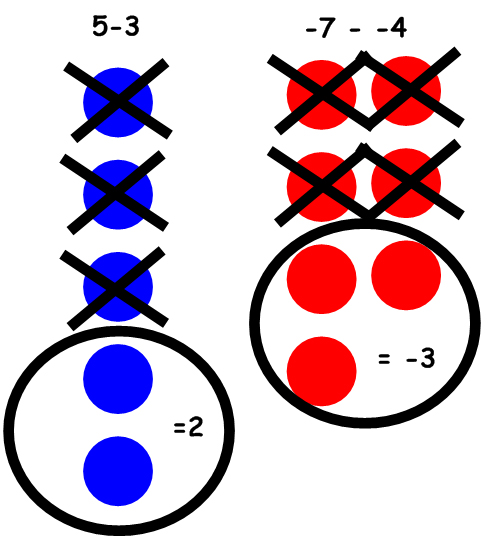
It is easy to draw a picture when you are subtracting integers that are the same sign. For example: 5-3=2, or -7 – -4 = -3. The pictures would look like below.
The problem comes when we start subtracting numbers of the opposite sign. At that point in time, it is just best to introduce the rule for subtracting. Trust me, if you understand addition of integers, you will appreciate how easy this rule is. When subtracting integers, you simply add the opposite of the second number. Here are some examples:
-6 – 5 : The 5 is positive, so we would rewrite our problem -6 + -5
7 – 9 : Again, the 9 is positive: so we’d rewrite it 7 + -9
8 – -6 : The 6 is negative, so we would rewrite it 8 + 6.
-2 – -3 : The 3 is negative, so we’d rewrite it -2 + 3.
From there, you follow the rules of addition:
1.) Signs same: Add the numbers and keep the sign
2.) Signs different: Find the difference, keep the sign of the larger number
Answering those problems:
Same Sign: -6 – 5 = -6 + -5 = -11
Different Sign: 7 – 9 = 7 + -9 = -2
Same Sign: 8 – -6 = 8 + 6 = 14
Different Sign: -2 – -3 = -2 + 3 = 1