Topics
1. Find Percent Given Part and Whole
2. Converting Measurements Using Ratios
Find Percent Given Part and Whole
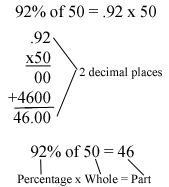
In previous lessons, we’ve learned how to find the percent of a number; say, if you scored 92% on a test with 50 questions, how many questions did you get correct? You end up multiplying the two like so:
But what if the question seems a little backwards. You got 36 questions correct on a test. This was a 90%. How many question were on the test? So you’ve been given the percentage, and the part, and have been asked to find the whole. To figure this out, you are basically setting up an equation:
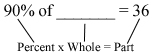The whole becomes an unknown, which we make a variable. You then set up the multiplication the same way you did for percent of a number. Convert the percentage to a decimal, and multiple. Your equation would then look like this:
.9a = 36
From there, simply remember our two key words for solving equations: OPPOSITE OPERATIONS, and you’re golden. The opposite of multiply is divide, so we’ll solve the equation like so:
Now to finish solving for our whole, the variable, we do need to divide with a decimal. This takes us back to our lesson on the frog and the dog. If you need a refresher on decimal division, click here. Our example problem would look like this:
Thus our unknown is 40. There are 40 question on the test. 90% of 40 = 36.
Converting Measurements Using Ratios
This is something we do on a fairly regular basis. I need 3 feet of a certain material, but it’s only sold by the inch, how many inches do I need? To be able to do this, we first need to know the basic unit rates.
12 inches / 1 foot
3 feet / 1 yard
36 inches / 1 yard
5280 feet / 1 mile
1760 yards / 1 mile
We may also be asked to do this with times as well.
60 seconds / 1 minute
60 minutes / 1 hour
24 hours / 1 day
365 days / 1 year
From there it’s just a matter of setting up a proportion. Let’s say I need 8 feet of a material, but the material is sold by inches. The proportion would be set up like this:
Notice how I have set up the proportion. I know I want to convert feet to inches, so I put the unit rate for the conversion I want on the left. On the other side, I have my unknown over how many feet I need. Note, I have the same units on top and bottom. Like all proportions, I have to have the same units on the top of both rations, and the same units on the bottom of both ratios, otherwise it will not work. From there, I can solve it as any proportion, by cross multiplying and solving the equation.
So, there are 96 inches in 8 feet. Here is another example.
How many seconds are there in 4.5 minutes?
So, there are 270 seconds in 4.6 minutes.