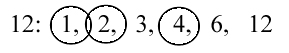Topics
1. Divide Decimals by Whole Numbers
2. Decimal Division
3. Prime Factorization
4. GCF
5. LCM
Divide Decimals by Whole Numbers
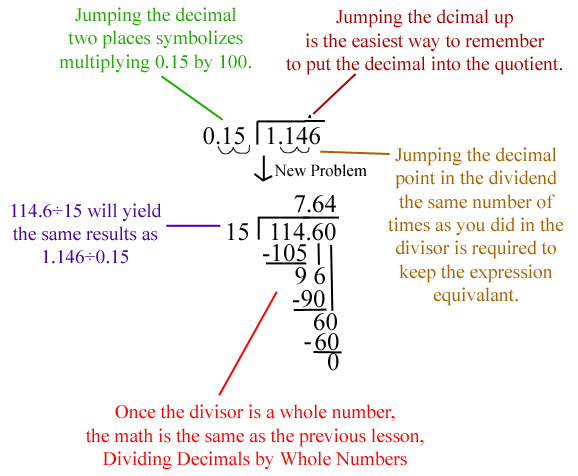
This is the lesson where we do away with remainders. No more will we say that a 30÷7=4r2. Nope. Now we follow a a bit more complex algorithm. Let’s take a look at 196÷32. With the old algorithm it would have looked like this:
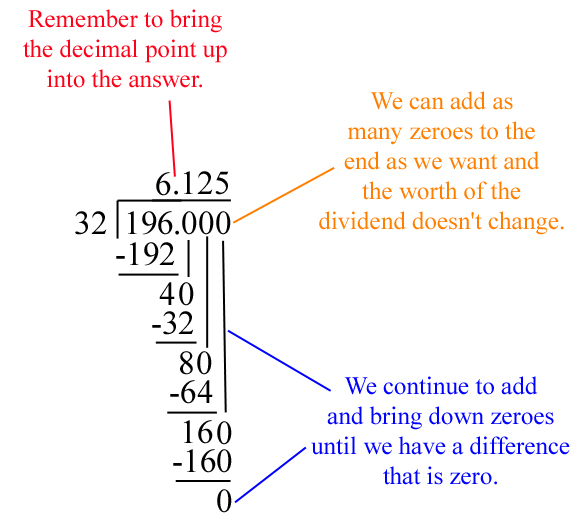
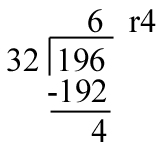One thing that we already know is that the decimal point in a whole number comes right at the end of it. So, 196 = 196.0. With this knowledge, we can now extend out our problem until we find a more complete solution. One key thing to remember, is wherever we put the decimal in the dividend (the number on the inside) we have to jump the decimal up into the answer at that same spot. It would look more like this:
There will be sometimes that we come across answers that seems to keep going on and on. If it is a repeating decimal, such as if you were to do 1÷3 which equals 0.333333333…., you can put a line over the first 3 and that tells us that number keeps repeating forever. It would look like this:
If it is not a repeating decimal, but still seems to not stop, then we can round it. Often times, the hundredth is the furthest we will ever need on a decimal. Remember though, to be able to round to the hundredth, we need to go one additional place so we know whether to round up or leave it the same. Anything less than 5 stays the same, anything 5 or greater rounds up. Let’s look at the original problem I mentioned, 30÷7. It would equal 4.28571….. To round to the hundredth, which is the currently the 8, we need to look at the digit one past it, which is a 5. A 5 tells us to round up, so our answer would be 4.29.
Decimal Division
To teach decimal division, I begin by telling the story of the Frog and the Dog. the kids each create a picture like the one below:
Once upon a time there was a dog who lived in a house. He was a pretty peaceful dog, but he was also scared of just about everything. He had a new neighbor move in. His new neighbor was a frog. Now, this was a mean, mean frog. The dog quickly became scared of the frog. Soon as the frog discovered this, he started to taunt the dog. He would jump at the dogs house. Each time he would jump toward the house, the dog would jump away. Eventually, the frog gets right up next to the dog’s house, and the dog gets so scared he jumps through the roof.
The first thing we need to know about dividing by a decimal, is that you can’t. This story teaches us how to change the problem from dividing a decimal into a problem where we divide multi-digit numbers instead. For a review on that lesson, go back to Lesson 5 on Week 6.
Like I said, we simply can’t divide by decimals, it’s much too difficult, and much easier to divide by whole numbers. The frog jumping towards the house represents multiplying the divisor by whatever power of 10 is necessary to make it a whole number. In the problem pictures above, you are dividing by 1.7 so you’d have to multiply it by 10 to make it 17. To keep the math correct, whatever we do to the number on the outside, we have to do to the number on the inside. This is represented by the dog jumping each time the frog does. The frog jumping through the roof is simply a reminder to put the decimal point up into the quotient as well. Here’s another example, without the frog and the dog intertwined with it:
Prime Factorization
Remember that a factor is either a number you multiply to get a product, or a number that evenly divides into another. Both mean basically the same thing, just worded a little different. For this lesson, we also need to remember that a prime number is a number that has only two factors 1 and itself. Though the list is endless, a few of the prime numbers are 2, 3, 5, 7, 11, 13, 17, and 19. A composite number is any number that has more than 2 factors: 4, 6, 8, 9, 10, 12, etc.
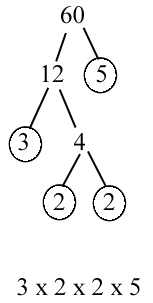
Prime factorization, then, is the prime numbers you would multiply together to get a certain product. For example, 15 is a composite number, but we could multiply the prime numbers 3 and 5 together to get it, so 15′s prime factorization is 3×5. A more complex example might be 60. 60=12×5, but 12 is not prime, so you need to break it down, 60=12×5=4x3x5. The numbers are still not all prime, so we need to break it down one further 60=4x3x5=2x2x3x5, so our prime factorization for 60 is 2x2x3x5. The easiest way to represent this process is through what we call a factor tree. The factor tree for 60 would look like this:
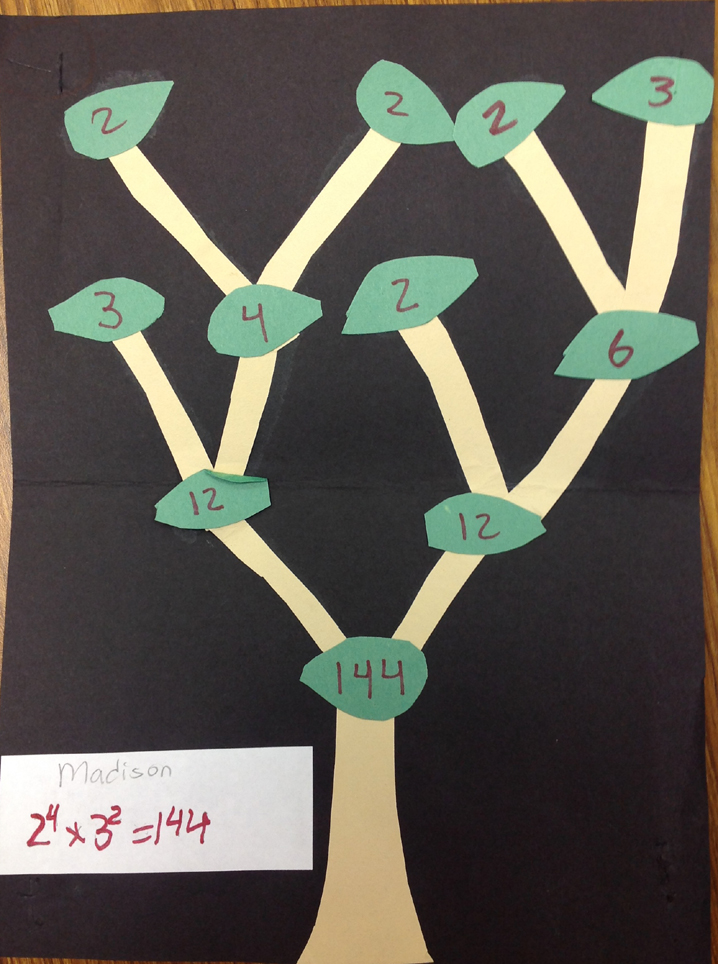
The students will practice this by selecting any number between 100 and 200 that has at least four prime factors, and creating a factor tree similar to what is pictured below:
Greatest Common Factor
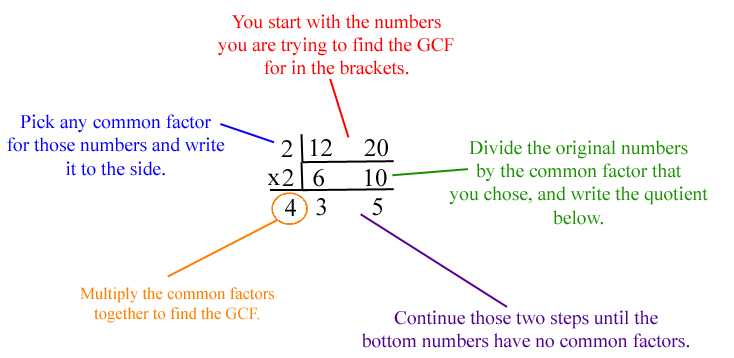
Greatest Common Factor, or GCF, is exactly what it sounds like it should be. Greatest, meaning largest, common, meaning same, and factor being a number that divides into another, the GCF will be the largest factor that two numbers have in common. Take the numbers 12 and 20. There are two different ways we can find the greatest common factor. The first would be by listing all the factors for the smaller number, and circling the ones that are the same as the larger.
The other way is pictured below. I like to call it the Cake Method. The steps are explained around it.
Least Common Multiple
Much like the GCF, if you understand the meaning of the words in Least Common Multiple, LCM, than you know what you’re looking for. Least meaning smallest, common meaning same, and multiple being a number you can get by multiplying by it. If we were to take our previous numbers, 12 and 20, and ask for the LCM of them instead, it would be 60. There are three different ways we can find this, the last one being the easiest in my opinion. First you could list out the multiples of the larger number. Once you get to a multiple that would be the same for both, you’ve found it. Listing multiples is like skip counting by that number.
20: 20, 40, 60
12 does not go into 20, so we keep listing. Same with 40. However, 12 does go into 60, so it’s our LCM. Another way is by finding the prime factorization of both numbers. This one is a little more difficult, but by multiplying by all of the prime factors of each number, you can find it as well. However, if there are common prime factors in each number, you only use that factor once. Here’s the example for 12 and 60:
I much prefer the final method, because once you understand the Cake Method for GCF, it looks exactly the same. The only difference is rather than just multiplying the numbers to the side, you multiply the numbers on the side as well as the numbers on the bottom. Example:
