Topics
1. Understand, Compare and Order Decimals
2. Add and Subtract Decimals
3. Multiplying Decimals
4. Factors, Multiples, and Divisibility
5. Multi-digit Whole Number Division
Add and Subtract Decimals
Adding and subtracting decimals is no different than adding and subtracting any multi-digit number. The key thing to remember is you have to line up the decimal points. From there, you just add from right to left, being sure to carry when needed. Remember, the decimal point in the answer is included in the aligning of the decimals.
Subtraction looks the exact same, except for rather than carrying the ones, you might have to borrow from the previous column. also shown in the subtraction problem, is what you would do with a whole number. When the decimal point is not shown in a whole number, it is assumed to come just behind the ones place. 33 = 33.0 Remember, we can add as many zeroes as necessary to the end of number to make a problem possible.
Multiply Decimals
Similar to adding and subtracting decimals, multiplying decimals is very similar to multiplying multi-digit numbers, with the small twist of the decimal point. In fact, when multiplying decimals, we ignore the decimal points in the beginning. 3.2×4.8 would be the same as 32×48 until the final steps. 32×48=1536. The final step is to count how many numbers there were past a decimal point in the original problem, and then count in that many places in the answer. 3.2 has one number past the decimal, as does 4.8, so in our solution, we count in two places from the right and put our decimal point into the answer, so 1536 becomes 15.36.
There is part of our practice that will simply ask us to do that final step.
Place the decimal point in each produce.
1.2 x 3.6 = 432.
Again, if we count, each of the numbers has one digit past the decimal point, so
1.2 x 3.6 = 4.32
An problem involving multiplying decimals would look as follows. Please pay careful attention to all of the side notes around it.
One final thing to make note of is multiplying by multiples of 10. If I multiply by 10, it simply moves the decimal points one place to the right. Just like 3×10=30, 3.2×10=32.
Factors, Multiples, and Divisibility
Factors – Numbers that are multiplied together to get a product; could also be defined as numbers that will evenly go into another.
Example: List the factors of 18. 18′s factors are 1, 2, 3, 6, 9, and 18. All of those numbers evenly divide into 18.
Multiples – The easiest way to think of multiples is if you were to count by a certain number.
Example: The multiples of 3 would be listed as if we were counting by 3s: 3, 6, 9, 12, 15, 18, 21, etc….
Divisible – If a number can be evenly divided by another
Example: 14 is divisible by 7 because 7 can go into 14 twice without a remainder.
Certain numbers have rules that will easily tell us if any number is divisible by it. Example, all even numbers are divisible by 2. Here are the rules that we must remember:
Multi-digit Whole Number Division
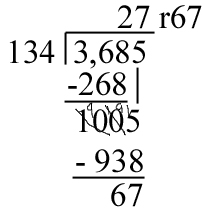The best tool to use when trying to solve a multi-digit multiplication problem as shown above is rounding. Working with easier numbers will make the whole thing more bearable. So, let’s say rather than 134, we’re working with 150. 150 does not go into 3, or 36, so we begin with 368. 150 goes into 368 twice, giving us the first step in the problem.
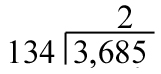You then multiply that 2 by 134 to get the 268 down below. Subtracting 268 is where you get the 100.
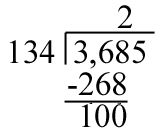We still have the unused 5 in the original problem. You bring down that 5 to end of the 100 to give you 1005, then it’s back to division, where the rounding comes in handy again. Round 134 up to 150 again. Because we’re rounding the 134 up so much, we want to give a little slack to the dividend, so we’ll round the 1005 up to 1050. 150 goes into 1050 7 times.
Again we follow this with the multiplication (7×134) and subtraction (1005-938).
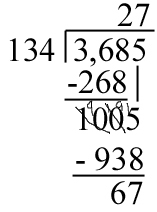134 does not go into 67. In the next lesson, we will learn how to continue on with the division adding a decimal point, but for today, we will simply leaves the remainder shown in the original problem. Keep in mind that after today, there will be very few problems where remainders are allowed, so marvel in them while you can.