With the change in plans this week, and Parent Teacher Conferences, it looks like we’re actually only going to have one math lesson this week. The week will look like this:
M – Reading Common Core Questions
T – Unit 1 Retest
W – Unit 2 Pretest
Th – Understanding, Compaing, and Ordering Decimals
F – No School (Comp Day)
Understanding, Comparing and Ordering Decimals
A decimal is considered any number that uses a decimal point.
Examples: 3.75, 21.6, 0.45, 5.76
Any of the numbers to the right side of the decimal represent only a part of a whole. If the number to the left of the decimal is just a zero, then the number you are dealing with is less than one.
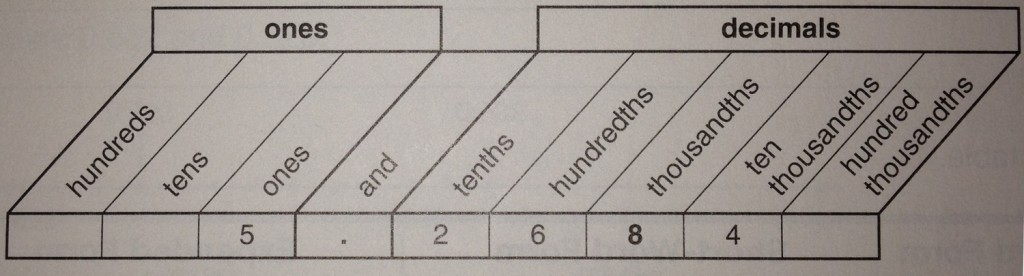
To fully understand decimals, we have to know how to say them, which means understanding their place values. It works very similar to whole number place value. Remember, ones, tens, hundreds, thousands, etc. Just think of them in reverse order, adding a ‘th’ to the end of each. Skipping the ones, decimal place values are tenths, hundredths, thousandths.
When it comes to reading decimals, the decimal point is said as an “and” to distinguish between the whole number and the decimal. 3.5 wold be said “three and five tenths”. 3.67 would be said “three and sixty-seven hundredths. The number in the picture above would be “five and two-thousand six-hundred eighty-four ten thousandths”.
When it comes to comparing decimal numbers, the key think you need to remember is to be sure you are comparing the same place between numbers. The easiest way to do this is to align the decimals vertically, lining them up at the decimal point, and then compare them once place at a time.
If you look in the ones place of those numbers, they are both 3, so the next step isto move one place to the right. If you look at the tenths place, the top number has a 2 and the bottom number has a 0. To correctly write the comparison for this we need to remember our comparison symbols:
> Greater than
< Less than
= Equal
The easiest way to remember which symbol to use is to think of them as a hungry alligator. The alligator would rather eat the bigger number, so it’s jaws should be opening toward the larger number.
Our original comparison would be written like this:
3.27 > 3.09
If the numbers were in the opposite order, than the sign would just flip with it:
3.09 < 3.27
You could also think of the decimals as numbers on a number line. Remember, as you move to the right on the number line, the numbers are greater in calue. As you move to the left, they decrease in value. If we were to compare 0.332 and 0.323 our number line would look like this:
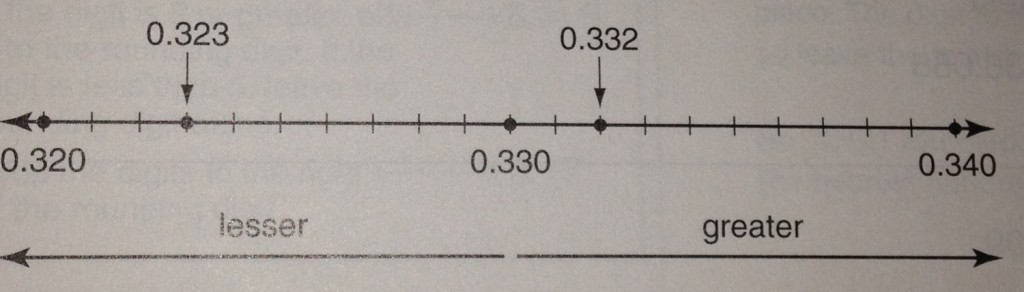As they are places, 0.332 is further right on the number line, therefore, it’s the larger number.
The final step in this lesson is ordering decimals. This skill is basically the same as comparing decimals, the only difference being you are comparing more than two decimals at a time. Let’s say we need to order 3.27, 4.86, 3.09, and 3.85. Aligning them vertically and comparing the places separately is the easiest way to go.
You would start with the ones place. Three of the four are the same, but the fourth has a 4 which tells us no matter what the decimals say, it’s going to be the largest. Comparing the tenths place for the remaining three, you have a 2, a 0, and an 8. those would arrange 0, 2, 8, which means ordering these from least to greatest would look like this:
3.09, 3.27, 3.85, 4.86
The final important step is to pay attention to which direction the question is asking to you to order it from, either least to greatest, or greatest to least. Beyond that, it’s pretty straight forward.