Topics:
1. Parts of a Mathematical Expression
2. Variables and Expressions
3. Properties of Equality
4. Combining Like Terms
Parts of a Mathematical Expression
To begin, knowing the parts of an expression is very heavy in knowing the vocabulary. Here is a list of the necessary vocab words with definitions.
addend – the numbers added in an addition problem’ 5 + 6 = 11
sum – the answer in an addition problem; 5 + 6 = 11
difference – the answer to a subtraction problem; 5 – 3 = 2
dividend – the first number in a division problem; 6 ÷ 3 = 2
divisor – the second number in a division problem; 6 ÷ 3 = 2
quotient – the answer in a division problem; 6 ÷ 3 = 2
factor – numbers multiplied together to get a product; factors might also be referred to as nunbers that will even go into another; 3 x 4 = 12; 3 and 4 both evenly go into 12, therefore, they are factors of 12
product – the answer in a multiplication problem; 3 x 4 = 12
monomial – a number, a variable, or a product of numbers or variables; a, 3, 5b, 7a²
polynomial – a group of monomials added together; 7a² + 3b + 6;
term – each of the monomials within a polynomial; 7a² + 3b + 6; Note: When referencing terms, subtraction is thought of as adding the negative, so if our polynomial were 6a – 3b, then the two terms would be 6a and -3b.
coefficient – the number a variable is being multiplied by; 3a, 4b; One thing to note with this is if a variable does not have a number multiplying it, like ‘c’, then it’s coefficient is 1 because there is only one c there.
——————————————————————————
There are also less commonly used words, but might be fun to know:
augend – the proper name for the first number in an addition problem; 3 + 4 = 7
minuen – the first number in a subtraction problem; 5 – 2 = 3
subtrahend – the second number in a subtraction problem; 5 - 2 = 3
multiplicand – the first number in a multiplication problem; 4 x 5 = 20
multiplier – the second number in a multiplication problem; 4 x 5 = 20
——————————————————————————
With these terms, the main goal is to be able to identify all of the separate parts within an expression. This skill will be checked in several ways. Here are some examples:
***How many terms are in the following expression?
7km + 4 + 7k + 8n + 8n³p
The hard part for the students is to look past the difficulty of the expression and simply answer the question. In that expression there are 5 terms, each of them separated by the addition sign.
***Name the terms in the following expression.
4qr – 8
Remembering that subtraction is considered addition of a negative, the terms in this expression are 4qr and -8.
***In the expression 12 + 46a³, what is the coefficient of a³?
Remember, you are looking for the number that the a³ is being multiplied by, so the answer to this question would be 46.
Variables and Expressions
This lesson has to do with the taking expressions from words into number form. A lot of the vocabulary from the previous lesson comes into play here because it requires knowing what they mean. Examples:
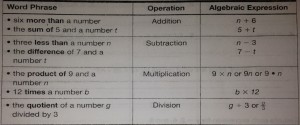Another aspect of this lesson, which we have already begun to work on as separate tasks, is taking a number and putting it in the place of a variable.
Example:
Evaluate the expression 9n for n = 3, 5, and 7.
To solve this, you would simply put the numbers in for the n. 9(3)=27, 9(5)=45, and 9(7)=63.
Properties of Equality
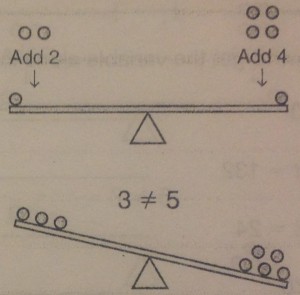
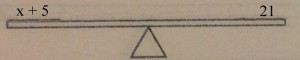
This lesson takes a closer look at that word equal and what it really means. We can think of an equation much like you would a scale where the middle of the scale is the equal sign. Let’s start with 1=1.
Currently the scale is balanced. We can make changes to that scale as much as we want, so long as we remember that whatever we add or subtract from one side, we have to do the exact same to both.
The most important part of this is remembering that bit. Whatever you do to one side, has to be done to the other, otherwise the expression is no longer equal.
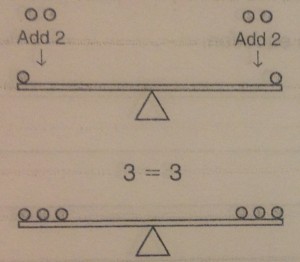
We use these properties of equality as we start moving into algebra as it is the key to keeping equations equal while solving for the variable. Let’s say we have the problem x+5=21, and we have been asked to figure out what x equals. To do this, we need to get the variable alone. We could think of this on the same scale.
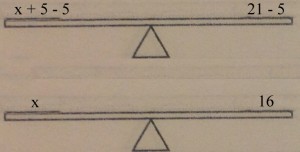
To get the variable alone, we need to get rid of the +5. The two key words are “opposite operation”. To get rid of a term like that we need to put it’s opposite on the scale. The opposite of +5 is -5. Remember though, whatever we do to one side, we have to do to both sides.
We’ve decided that x=16. We could then go back and check our answer by putting 16 in for the x in the original equation. 16+5=21 is true, so our answer is correct. These same rules apply for all operations, so knowing the opposites is one of the most important parts of this lesson. The opposite operations are addition and subtraction, and multiplication and division.
Combining Like Terms
Combining Like Terms is a process used to simplify an expression or an equation using addition and subtraction of the coefficients of terms. Consider the expression 5 + 7. By adding 5 and 7, you can easily find that the expression is equivalent to 12
The key to understanding Combining Like Terms is the meaning of the phrase like terms and being able to identify them. Here are a few examples of like terms:
***The following terms are like because they have just one variable, x, with a coefficient:
2x, 45x, x, -26x, -2x
***The following terms are like because they are all just simple numbers:
15, -2, 27, 2046, 0.6
***The following terms are like because they are y² with a coefficient:
3y², y², -y², 26y²
Please note that terms with exponents are not like terms without, so 5x² is not a like term to 3x.
Algebraic expressions can also be simplified by combining like terms. consider the equation
12x + 7 + 5x
Because 12x and 5x have the same single variable with only a coefficient, they are like terms and can be added together. 12+5=17 so 12x+5x=17x. The expression would be simplified to
17x+7
Here is a more complex example:
5x2 + 7x + 2 – 2x2 + 7 + x
The commutative property tells us we can rearrange the addition² without consequence. This can help us to put like terms together.
(5x² - 2x²) + (7x + x) + (2 + 7)
We can then simplify it by doing the basic operations between the like terms.
3x² + 8x + 9
Thank you Mr. Pratt for taking the time and going to all the effort to make the blogs, especially this math blog. It has been more time than I like to admit from when I was in school and I certainly do NOT remember math like this. Without this to reference it would be next to impossible to help J. with his homework.